지난 포스팅에 이어 주응력에 대해 정리해보자.
https://freeengineer.tistory.com/21
평면응력의 응력변환
▶평면응력 Plane Stress 평면응력은 지난번에 설명했듯이...아래와 같다. https://freeengineer.tistory.com/18 평면응력/탄성계수와 전단계수의 관계/평면응력의 후크의법칙/Plane stress/Relation of elastic modulus a
freeengineer.tistory.com
주응력이란 뭘까. 주응력은 영어 그대로 주요응력이란 뜻? 그정도다. 그럼 주응력이 평면응력내에서 의미하는 바가 뭘까?
위 링크에서 평면응력성분을 소개하였고, 평면응력의 회전된 축에서의 응력 공식을 배웠다. 이게 다 주응력과 최대 전단응력을 구하기 위한 과정이다. 주응력은 평면응력 상태의 사각요소를 회전시켜서 n, t 축으로 변환된 수직응력과 전단응력을 구하고, 구한 값들 중 최대 값과 최소 값을 주 응력이라고 한다. 여기서 최소 값은 음수의 최대 값을 의미하므로, 즉 인장, 압축 응력에 대한 최대 값을 구한다고 보면된다.
위 링크에서 설명한 평면응력상태의 사각요소가 회전된 상태에서 갖는 응력성분 공식을 아래와 같이 가져왔다.

sigma_n과 tau_nt성분은 모두 주기를 갖는 삼각함수(sin, cos)임을 주목해보자. 얘네들은 어짜피 꼬불꼬불 아래와 같은 형상의 그래프를 갖는다. 고등학교 댕기면서 미 적분을 배웠으니 활용해보면, 아래 함수에서 극대점과 극소점은 각 그래프를 미분했을때 기울기가 0이 되는 각도에서 발생한다. 즉 주응력 각도는 미분해서 알 수 있다. 이와 마찬가지로 최대 전단응력의 위치도 미분해서 0이 되는 각도를 찾으면 된다. 참고로 각도가 정의되는 범위는 -90도~90도 사이임을 주목하자~(-180~180도 아니다)

위 sigma_n의 식을 미분해보면 다음과 같다.
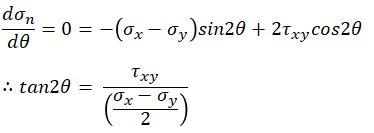
그리고 위 sigma_n의 함수는 180도의 주기를 갖는 주기함수이므로 또 다른 주응력은 위 식에서 나온 theta값에 대해 ±90도를 하면 구할 수 있다.(주응력의 위치에서 90도 평행이동 한 위치가 극소점 또는 극대점을 갖을거라는 의미)
위 미분을 통한 탄젠트 식을 축 좌표계로 표현해 보면 다음과 같다.(아래 좌표계의 각도가 2theta임을 주목하자. 두번쨰 주응력 값은 90를 이동한 값이 아니라 180이동한 값이다.)
아래와 같이 R값이 정의된다.

여기서 두개의 주응력의 방향은 위 좌표계를 통해 다음과 같이 정의할 수 있다. 두 주응력의 각도를 theta1과 theta2로 표현했다.
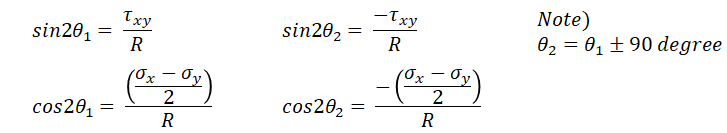
위 식을 R과 함께 이 포스팅 맨 위에 나온 sigma_n과 sigma_t에 대입하여 정리하면 주응력은 다음과 같이 정리된다.


어우 사실 주응력은 피로때문에 보통 중요하고 이거보다 최대전단응력 구하는게 더 중요하다. 너무 길어지니깐 다음에 최대전단응력을 구해보자. 그리고 나중에 이거 가지고 원을 하나 그리는데 모어원이라고 한다. 주응력 방향과 최대 전단응력 방향을 쉽게 구하기 위한 원인데, 사실 더 복잡한거 같다. 이만. 손아프다.
이어 쓴다. 최대전단응력을 구해보자.
위의 Figure.1에서 tau_nt에 대해 최대 값을 구해야 한다. 이 방식은 위에서 sigma_n의 최대값을 구하기 위해 각도 theta에 대해 미분을 하고 그 기울기가 0인 지점을 찾는 방식과 동일하다. 이를 아래와 같이 풀이하면,

다음과 같고 이를 Figure.2에 나타낸 좌표축에 중첩시키면 다음과 같다.

주목할 점은 주응력의 방향(파란색 선)과 최대전단응력의 방향(녹색 선)이 45도 각도를 갖는다는 것이다. (위 좌표는 2theta이므로 90의 각도는 45도 각도를 의미함.)
위 주응력을 구한 방식과 동일하게 최대전단응력을 구하기 위해 figure.4의 좌표축을 통해 sin, cos값을 구한다.

이를 원식에 넣고 tau_nt, tau_tn에 대해 풀이하면 다음과 같이 최대전단응력을 구할 수 있다.


추가로 다음의 규칙을 정리할 수 있다.
1. 주응력이 존재하는 회전각도에서는 전단응력이 존재하지 않는다. 이는 Figure.1의 tau_nt에 theta를 직접 대입해보자

2. 최대전단응력이 존재하는 회전각도에서는 수직응력이 존재하고 이는 평균응력이다.

3. 최대 전단응력의 각도는 주응력 각도의 ±45도 방향이다.

이 다음은 모어원이다.
'[Material Dynamics] 재료역학' 카테고리의 다른 글
| 모어 원(Mohr circle) (0) | 2023.04.12 |
|---|---|
| 평면응력의 응력변환 (0) | 2023.04.04 |
| 3차원 응력성분/3차원 후크의 법칙 (0) | 2023.03.12 |
| 평면응력/탄성계수와 전단계수의 관계/평면응력의 후크의법칙/Plane stress/Relation of elastic modulus and she (0) | 2023.03.02 |
| 경사면에 작용하는 응력/Stress on an inclined plane (0) | 2023.02.27 |